下の図のような、同じ大きさの正方形からなるマス目があり、12個の正方形には対角線が引かれています。 図の正方形の辺や対角線をたどって、最短距離（きょり）でAからBまで移動する経路の選び方は全部で①通りあります。 また、最短距離でAからCまで移動する経路の選び方は全部で②通りあります。
解答
①6 ②70
正方形のマス目を下の段から順に1段目、2段目…と呼ぶことにすると、最短距離でAからB、Cまで進むためには、1段目と3段目では必ず斜めに進まなくてはならない。 その点に気をつけながら、各頂点で一つ手前までの道順を順に足していけばよい。 ①ABは6通り、②ACは70通り。
（別解）ある頂点からいずれかの辺を通って次の頂点に進むことを1手と呼ぶことにすると、ACを最短距離で進むには、1段目と3段目で斜めに進まなくてはならないので8手が必要となる。 その8手のうち上の段に進むには、の順に4手が必要になる。 8手のうち4手を選ぶ方法は、
閉じる
解答
答え
①6 ②70
正方形のマス目を下の段から順に1段目、2段目…と呼ぶことにすると、最短距離でAからB、Cまで進むためには、1段目と3段目では必ず斜めに進まなくてはならない。
Bは6通り、②A
Cは70通り。
その点に気をつけながら、各頂点で一つ手前までの道順を順に足していけばよい。
①A
（別解）
Cを最短距離で進むには、1段目と3段目で斜めに進まなくてはならないので8手が必要となる。
の順に4手が必要になる。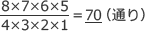
ある頂点からいずれかの辺を通って次の頂点に進むことを1手と呼ぶことにすると、A
その8手のうち上の段に進むには、
8手のうち4手を選ぶ方法は、
閉じる